Arm-Z: ekstremalnie modularny hiperredundantny ekonomiczny manipulator – opracowanie metod sterowania oraz analiza efektywności
Wstęp
Proponowany projekt koncentruje się na: koncepcji, projektowaniu, modelowaniu oraz sterowaniu strukturami rurowymi złożonymi z przystających modułów (ang. pipe-like modular systems, w skrócie PMS). W największym skrócie, dla takich oto czterech powodów:
- Rura to prosty i względnie łatwy do wykonania element konstrukcyjny, szczególnie efektywny w przypadku zginania wieloosiowego. Zachodzi ono w elementach uniwersalnych, to jest takich w których kierunek zginania nie może być z góry założony.
- Konstrukcje rurowe w swojej naturze, pozwalają na tworzenie kanałów komunikacyjno-transportowych, jak pokazano na Rys 1.
- Modularność to racjonalny sposób ekonomizacji konstrukcji. Pozwala ona na masową produkcję stosunkowo skomplikowanych identycznych elementów przy względnie niskiej cenie. Ponadto, modularność pozytywnie wpływa na odporność konstrukcji na awarie. Mianowicie, zużyty lub zepsuty element może być stosunkowo łatwo wymieniony przez identyczny odpowiednik.
- Responsywność, adaptowalność, rekonfigurowalność, szybka instalacja i dynamiczne sterowanie – to poważne wyzwania nowoczesnej architektury, budownictwa i inżynierii w wiecznie-zmieniającym się środowisku. Współczesne konstrukcje nie tylko muszą spełniać wymagania nośności i bezpieczeństwa, ale powinny również w sposób inteligentny dostosowywać się do zmiennego zarówno środowiska jak i wymagań użytkowników.

Rys. 1. Po lewej: wybrane kroki ciągłego rozkładania 40-to elementowego kołnierza z przystających elementów „obchodzących” Moduł Zarya na Międzynarodowej Stacji Kosmicznej. Odcień zabarwienia elementów koresponduje ze stopniem otwarcia. Czerwony i błękitny odpowiednio wskazują na w pełni zamknięty i otwarty stan. Dla każdego stanu podano stopień otwarcia w lewym dolnym rogu. W środku: wizualizacja koncepcji bazy w ekstremalnym środowisku w układzie „banana-split”. Po prawej: (modularny?) system oczyszczania powierzchni wody z wycieku ropy naftowej w ofercie Canadyne Technologies Inc.
Zarys koncepcji PMS
Systemy Ekstremalnie Modularne (ang. Extremely Modular Systems, w skrócie EMS) [1] to rodzina koncepcyjnych systemów konstrukcyjnych składających się wyłącznie z jednego typu modułu pozwalających na tworzenie konstrukcji o dowolnym kształcie. Jednym z takich systemów jest Pipe-Z (PZ) opisane w [2] i ostatnio zaproponowane jako system do szybkiej instalacji np. w stacjach orbitalnych czy kołnierzach ewakuacyjnych w przestrzeni kosmicznej [3], jak pokazano na Rys. 1.
Rozwinięciem PZ jest Arm-Z (AZ), czyli koncepcja hiperredundantnego manipulatora robotycznego składającego się z przystających modułów posiadających jeden stopień swobody (1-DOF) i realizującego (prawie) dowolne ruchy w przestrzeni [4]. Dwie zasadnicze zalety EMSów to: ekonomizacja (dzięki masowej produkcji identycznych elementów) oraz odporność na awarie (po pierwsze – zepsute moduły mogą być łatwo zastąpione, po drugie – nawet gdy jeden lub więcej modułów ulegnie awarii – manipulator taki może ciągle wykonywać, prawdopodobnie w stopniu ograniczonym, zakładane zadania). Natomiast podstawową wadą systemów EMS jest ich nieintuicyjne „składanie” oraz bardzo trudne sterowanie. Innymi słowy, połączenie koncepcji nietrywialnego modułu z formowaniem praktycznych konstrukcji oraz sterowanie ich rekonfiguracją (transformacją ze stanu A do B) są bardzo trudne obliczeniowo. Mimo to, prezentowane tutaj podejście jest racjonalne, zważywszy powszechną dostępność do wielkich mocy obliczeniowych w kontraście z wysokimi kosztami i „delikatnością” niestandardowych rozwiązań i urządzeń.
Skalowalność PMS
Koncepcja PMS może mieć zastosowanie w zagadnieniach projektowych o różnych skalach, np.:
- Robotyczny hiperredundantny manipulator do zadań w trudnych warunkach, w szczególności w środowisku niebezpiecznym dla życia i zdrowia człowieka.
- Elementy architektoniczne takie jak kolumny spiralne o sterowalnych parametrach (długość łuku spirali, krzywizna i skok), jak pokazano na Rys. 2.
- Stacje badawcze w środowiskach ekstremalnych (Rys. 1).
- Systemy do oczyszczania powierzchni wody z wycieku ropy naftowej. Takie urządzenie mogłoby zostać zrzucone ze statku powietrznego zaś kontrola globalnego kształtu mogłaby odbywać się na bazie zjawiska lokalnej samoorganizacji modułów reagujących na stan środowiska (czyste/zanieczyszczone) oraz przyległych modułów.
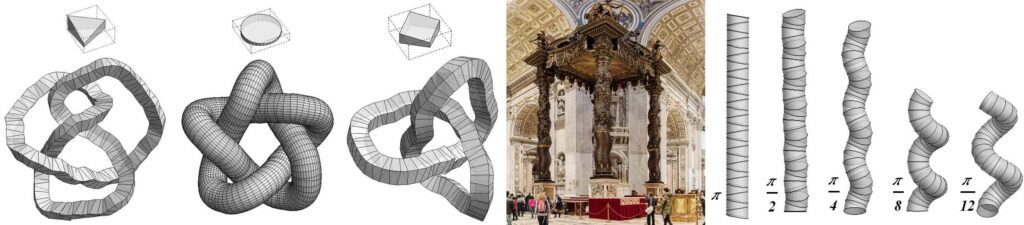
Rys. 2. Po lewej: Różne rodzaje węzłów matematycznych skonstruowanych z przystających modułów: Ósemka (41), Pięciolistnik (51) i Trójlistnik (31). W środku: historyczny przykład kolumny spiralnej: Baldachin w Bazylice św. Piotra (AD 1634, arch. Bernini). Po prawej: przykłady sterowalnych kolumn spiralnych skonstruowanych z identycznych modułów o różnych względnych skrętach (wartości skrętów pokazano).
1. Cel naukowy projektu
Celem naukowym projektu jest określenie kryteriów oceny globalnej efektywności PMSów, stworzenie algorytmów optymalizacji modułu bazowego oraz optymalizacji sterowania PMSem. W szczególności:
- Opracowanie modułu bazowego PMS pod kątem strukturalnym i funkcjonalnym w kierunku proponowanych obszarów zastosowań. Własności globalne PMS są określane poprzez własności poszczególnych (identycznych) modułów, co implikuje szereg nietrywialnych zagadnień badawczych:
- Jaki jest zakres ruchów PMS i jak w sposób efektywny może on penetrować przestrzeń wokół siebie?
- Jaka jest precyzja sterowania poprzez dyskretne skręty względne (jak przypadku silników skokowych)?
- Jakie są fizyczne, mechaniczne ograniczenia odnośnie stabilności i wytrzymałości takiej wielomodułowej konstrukcji i jak globalna struktura PMS ma się do lokalnej struktury modułu bazowego?
- Jak skonstruować połączenie skrętne między modułami by równocześnie przenosiły założone obciążenia?
- Jak inteligentnie modelować naprężenia/odkształcenia tej hierarchicznej konstrukcji?
- Jaką miarę zastosować do oceny tych i prawdopodobnie innych kryteriów w celu znalezienia najbardziej uniwersalnego rozwiązania?
- Sformułowanie matematyczne oraz optymalizacja dynamicznego przejścia między różnymi konfiguracjami PMS. Połączone w łańcuch moduły bazowe tworzą globalny kształt którego zadaniem jest dynamiczne przejście z obecnego stanu do zadanego. Ponieważ PMS jest wysoce nieliniowy, tego typu zagadnienie nie jest dostatecznie zbadane w piśmiennictwie naukowym poświęconym teorii sterowania. Ponadto, klasyczne techniki sterowania nie mogą być zastosowane w takim przypadku, przeto proponujemy zastosowanie alternatywnych metod (w tym heurystycznych) w celu sterowania w czasie rzeczywistym ogólnego kształtu PMS.
- Fizyczny demonstrator posłuży jako kontroler podający globalny stan PMS do komputera w celu analizy i wykonania procesu transformacji globalnego kształtu PMS do pożądanej konfiguracji, oraz jako najbardziej intuicyjny i przekonujący sposób zilustrowania efektywności proponowanych algorytmów.
2. Znaczenie projektu
- W zakresie mechaniki konstrukcji, w ramach projektu przeprowadzona będzie lokalna optymalizacja konstrukcji modułów. W literaturze są dostępne publikacje dotyczące topologicznej optymalizacji konstrukcji periodycznych (np. [5]) o różnym charakterze periodyczności (translacyjna, rotacyjna itp.). We wszystkich znanych nam doniesieniach periodyczność (a zatem i globalna konfiguracja konstrukcji) jest jednak ściśle określona. Niniejszy projekt dotyczy natomiast konstrukcji modularnych składających się z nieznanej z góry liczby modułów połączonych w nieznaną z góry konfigurację globalną. Liczba takich konstrukcji zależy wykładniczo od liczby modułów, a zatem techniki stosowane w optymalizacji konstrukcji periodycznych mają zbyt dużą złożoność czasową. Zaproponujemy nowatorskie rozwiązanie polegające na reprezentacji problemu globalnej optymalizacji w równoważnej postaci problemu lokalnej optymalizacji pojedynczego modułu poddanego wielu lokalnym wymuszeniom brzegowym.
- W obszarze teorii sterowania, proponowane badania są kontynuacją rozpoczętych już prac, jednak idą w kierunku zarazem bardziej ogólnym i złożonym, mianowicie:
- wprowadza moduły bazowe o podstawie okrągłej (ciągłej) w miejsce podstawy wielokątnej (dyskretnej), co implikuje zamianę obrotowego ruchu skrętnego skokowego na ciągły.
- wprowadza za zagadnienie auto-kolizji (w poprzednich pracach rozpatrywane PMSy były na tyle krótkie, że problem ten mógł być pominięty).
- wprowadza zagadnienie odporności na awarie, innymi słowy, intencją naszą jest wykazać, iż przewagą prezentowanego rozwiązania jest to że możliwe jest realizowanie (częściowo?) danego zadania nawet mimo uszkodzonego jednego lub więcej modułów. Oczywiście algorytm sterowania będzie musiał uwzględnić awarie tego/tych modułów w sterowaniu globalnym kształtem PMSa.
- W obszarze teorii projektowania, wprowadza zagadnienie kinematycznych modularnych elementów architektonicznych. Dotychczasowe badania na ogół koncentrują się na rozwiązaniach silnie nie-modularnych (niestandardowych).
3. Koncepcja i plan badań
- Analiza potencjalnych obszarów zastosowań oraz rozpoznanie wyzwań technologicznych w projektach o charakterze architektonicznym i inżynieryjnym. W szczególności:
- Ergonomia rekonfigurowalnych habitatów wymusza dopuszczalne zakresy średnic i innych wymiarów modułów by możliwe było zaprojektowanie obiektów na potrzeby stałego lub czasowego pobytu ludzi czy zwierząt, tudzież obiektów o funkcjach dodatkowych, które też muszą być bezpieczne i funkcjonalne.
- Konstrukcje w środowiskach ekstremalnych (tak habitaty jak i manipulatory) muszą dodatkowo spełniać rygorystyczne wymagania ochrony termicznej i/lub radiacyjnej. Będzie to miało decydujący wpływ na grubość ścian (ścianek) modułów bazowych.
- W przypadku architektonicznych modularnych elementów kinematycznych, istotne jest określenie zakresów obciążeń jakie mają być przenoszone. Wpłynie to w sposób oczywisty na dobór materiału oraz wewnętrzną strukturę modułu bazowego.
- Środowisko pracy oraz rodzaj zadań dla manipulatora wpływają zarówno na jego fizyczne rozmiary i ruchomość oraz dopuszczalną masę głowicy roboczej, tudzież sił i momentów przyłożonych na czele manipulatora. Rys. 3 ilustruje iteratywny charakter procesu projektowania PMSów.
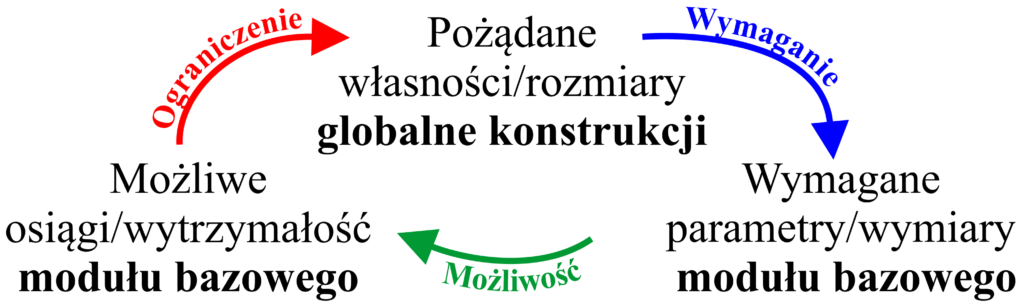
Rys. 3. Pętla projektowa: cykl ilustrujący sprzężenie między lokalną i globalną optymalizacją PMSów.
- Optymalizacja strukturalna modułu oraz określenie mechanicznych ograniczeń całej konstrukcji. Zadania opisane powyżej dotyczą geometrycznych cech i przekształceń konstrukcji PMS. Zadanie to poświęcone jest mechanicznej analizie konstrukcji PMS oraz optymalizacji jej pojedynczych modułów. Planujemy w szczególności:
- Stworzyć hierarchiczny model konstrukcji wykorzystujący modularny charakter PMS, metodę elementów skończonych oraz metody redukcji modelu [6]. Celem jest opracowanie efektywnego numerycznie modelu dwupoziomowego: poziom wyższy opisywałby globalną konstrukcję w kategoriach brzegowych stopni swobody związanych z interfejsem pomiędzy poszczególnymi modułami reprezentowanymi w sposób skondensowany, podczas gdy poziom niższy opisywałby lokalnie pojedyncze moduły konstrukcji poddane wymuszeniom brzegowym. Ewentualne wymuszenia wewnętrzne modułów na poziomie globalnym będą redukowane do wymuszeń brzegowych stopni swobody.
- Zaadaptować metodę konstrukcji bazowej (ang. ground structure) [7] i przeprowadzić topologiczną optymalizację konstrukcji pojedynczego modułu. Liczba różnych globalnych konfiguracji konstrukcji PMS rośnie wykładniczo wraz ze wzrostem liczby modułów, globalna optymalizacja PMS jest więc zadaniem numerycznie zbyt czasochłonnym. Naszym celem jest wykorzystanie powyższego modelu hierarchicznego w celu opracowania lokalnej reprezentacji różnych geometrycznych konfiguracji PMS w równoważnej postaci zbioru lokalnych obciążeń brzegowych pojedynczego modułu. Tego typu reprezentacja umożliwi wykorzystanie zaadaptowanej metody konstrukcji bazowej i przeprowadzenie lokalnej optymalizacji topologicznej modułu poddanego wielu niezależnym obciążeniom. Iteracyjne metody optymalizacji pozwolą rozwikłać spodziewaną zależność obciążeń brzegowych i wewnętrznej topologii. Przykładowa konstrukcja bazowa została przedstawiona na Rys. 4.
- Oszacować istotne mechaniczne ograniczenia funkcjonalności PMS o zoptymalizowanych modułach. Rozważymy kryteria takie jak maksymalny zasięg konstrukcji (tzn. maksymalna liczba modułów), maksymalne obciążenie oraz przyspieszenie podczas przekształceń geometrycznych ze względu na ograniczenia związane z maksymalnym naprężeniem efektywnym lub ściskającym.
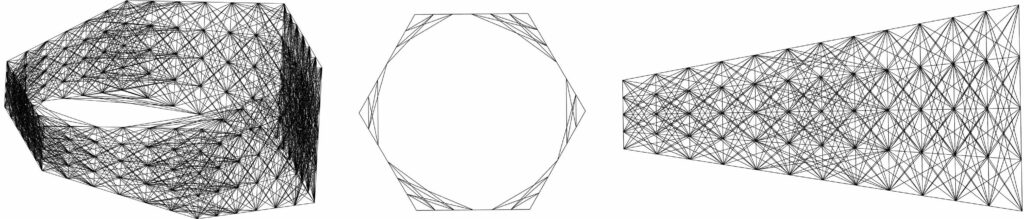
Rys. 4. Przykład konstrukcji bazowej modułu bazowego. Widok aksonometryczny, plan i widok z boku.
- Algorytmy sterowania hiperredundantnym robotycznym manipulatorem typu „trąba słonia”. Jednym z podstawowych problemów transformacji PZMów jest zginanie w szczelinie opisanie w [8]. Stan początkowy to rura prosta, zaś końcowy, torus. Cała transformacja powinna zawierać się w szczelinie o minimalnej szerokości. Przykładowe zginanie w siedmiu dyskretnych krokach 16-to modułowego PMSa obliczonego przy pomocy optymalizacji rojem cząstek (PSO) pokazano na Rys. 5. Znacząco ciekawszy i bardziej złożonym problem zdefiniowano w sposób następujący: znajdź transformację PMSa od stanu początkowego do końcowego, takiego że czoło PMSa znajdzie się najbliżej jak to możliwe do zadanego punktu w przestrzeni. Dodatkowo nałożono ograniczenia: chybotliwość czoła ma być minimalna, oraz zabronione są kolizje z otoczeniem. W prezentowanym w [8] przypadku problem auto-kolizji nie występuje, gdyż PMS nie jest wystarczająco długi. Rys. 6 ilustruje rozwiązanie obliczone również przy pomocy PSO.
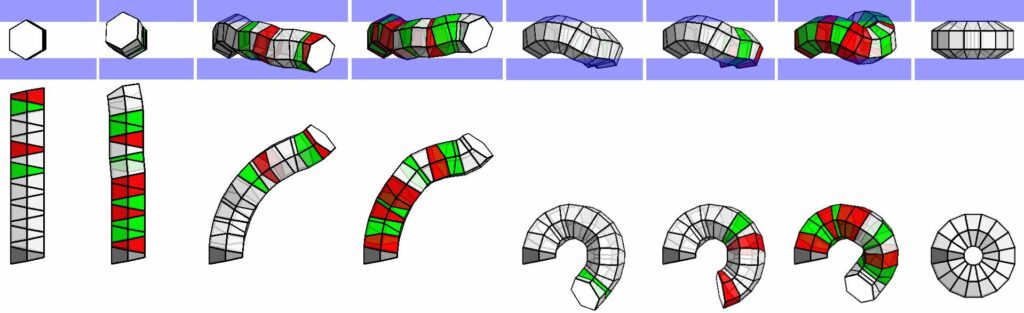
Rys. 5. Najlepsze rozwiązanie dla 16-to modułowego PMSa złożonego z sześciokątnych modułów bazowych z „rura prostej” do pełnego torusa. Zielony i czerwony wskazują odpowiednio: skęcenie danego modułu w prawo i lewo.

Rys. 6. Najlepsze rozwiązanie znalezione przy pomocy PSO dla 12-sto moduowego PMSa. Wybrane kroki z 17-sto krokowej transformacji. Konwencja kolorystyczna jak w Rys. 5.
Jak wspomniano, rozmiary, a co za tym idzie – zasięg takiego modularnego manipulatora zależy od planowanej funkcji, np.: spawanie, czyszczenie, inspekcja wizualna, itp. Należy podkreślić, że istniejące rozwiązania w tym zakresie są niezwykle ograniczone. Obecnie funkcjonujących jest tylko kilka takich urządzeń, w dodatku na etapie raczej eksperymentalnym. Rys. 7 pokazuje znane nam przykłady. Należy zaznaczyć, że owe rozwiązania są również poniekąd modularne, niemniej w niniejszym projekcie koncepcja modularności jest realizowana w stopniu o wiele głębszym, można powiedzieć – ekstremalnym. Dodatkowo, sposób sterowania jest fundamentalnie inny. W proponowanym projekcie każdy moduł bazowy ma tyko i wyłącznie 1DOF, zaś ruchomość manipulatora wynika z synergii między nimi.

Rys. 7. Przykłady najbardziej manipulatorów typu „trąba słonia”. Górny rząd: Festo (12 DOF) i dwa manipulatory OC Robotics.
Dolny rząd: ramiona OC Robotics w trakcie spawania laserem.
- Analiza eksperymentalna oraz konstrukcja stanowiska badawczego/demonstratora. Istotną częścią projektu jest wykonanie fizycznego demonstratora – modularnego manipulatora rurowego. Będzie służył on dwojako:
- jako urządzenie przekształcające stan systemu, uzyskany poprzez pracę manualną operatora, do postaci cyfrowej, która będzie dalej analizowana w środowisku programistycznym;
- jako konceptualny prototyp PMS, realizujący algorytmy sterujące w rzeczywistości i w konsekwencji wpływający na ich dostrojenie. Taki demonstrator posłuży jako dowód poprawności podejścia, pokaże użyteczność PMS i posłuży jako podstawa do prac nad badaniami o charakterze aplikacyjnym. Planuje się zbudowanie trzech manipulatorów o różnej długości (ok. 12, 24, 36) i geometrii. Zbudowane będą w ramach koncepcji Internetu Rzeczy (Internet of Things – IoT). Oznacza to, że każdy moduł będzie posiadał swoje własne niezależne sterowanie jak i źródło energii.
4. Metodyka badań
- W obszarze mechaniki konstrukcji, istotnymi zadaniami badawczymi są:
- opracowanie metody reprezentacji zbioru konfiguracji globalnych konstrukcji modularnej w postaci zbioru lokalnych obciążeń brzegowych pojedynczego modułu oraz
- adaptacja i zastosowanie wybranej techniki optymalizacji konstrukcji do wynikłego stąd zadania lokalnej optymalizacji modułu poddanemu wielu niezależnym obciążeniom. Wykonamy przegląd metod redukcji modelu [6] i wybraną metodę wykorzystamy w celu budowy hierarchicznego, dwupoziomowego modelu konstrukcji PMS. Poziom globalny będzie opisywał konstrukcję w kategoriach brzegowych stopni swobody tworzących interfejsy pomiędzy kolejnymi modułami, podczas gdy poziom lokalny zredukuje odpowiedzi brzegowych stopni swobody do lokalnych wymuszeń pojedynczego modułu. Ponieważ wszystkie moduły są przystające, otrzymamy w ten sposób lokalną reprezentację konfiguracji globalnej. Na potrzeby lokalnej optymalizacji modułu poddanego takim wymuszeniom brzegowym zaadaptujemy i wykorzystamy metodę konstrukcji bazowej (ang. ground structure) [7]. Sprzężenie pomiędzy wewnętrzną topologią modułu a wymuszeniami brzegowymi będzie wymagało zastosowania technik iteracyjnych.
- W obszarze sterowania rekonfiguracją globalnego kształtu PMS, szereg algorytmów zostanie zaproponowanych i przeanalizowanych. Algorytmy te będą oparte o istniejące techniki gradientowe, metaheurystyki (algorytmy ewolucyjne: EA, PSO) itp., wzmocnione techniki uczenia, sieci neuronowe i inne metody sztucznej inteligencji (AI), które zostały już skutecznie zastosowane do innych typów manipulatorów typu „trąba słonia”. Badania w tej części:
- skoncentrują się na efektywnej reprezentacji potencjalnych rozwiązań, oraz na
- „dostrajaniu” parametrów algorytmów. W celu oceny jakości i efektywności każdego podejścia, planowane jest symulacyjne przetestowanie znaczącej liczby różnych scenariuszy zastosowania PMS. W ramach tych scenariuszy znajdą się typowe zastosowania PMS jako manipulatora, ale także inne interesujące możliwości. Między innymi, rozważane będą:
- przeniesienia czoła manipulatora z punktu A do B;
- transport głowicy zamontowanej na manipulatorze w małych, wąskich przestrzeniach z bardzo ograniczoną możliwością ruchową;
- z dynamicznie przemieszczającymi się przeszkodami, kontaktów z którymi należy unikać;
- wszystkie w/w wraz z narzuconymi więzami i kryteriami optymalizacyjnymi (np. minimalizacja chybotliwości, itp.)
- inne scenariusze, które zostaną zdefiniowane w trakcie trwania projektu. Wszystkie algorytmy będą testowane w fazie numerycznych eksperymentów w celu znalezienia najlepszego rozwiązania wg założonej miary jakości. W celu przeprowadzenia tych testów w rozsądnym czasie, wymagana jest efektywna implementacja proponowanych algorytmów oraz metod kodowania rozwiązań. W szczególności, niezbędne będzie napisanie odpowiedniego oprogramowania wykorzystującego możliwości kart GPGPU. Istotnym aspektem badań w ramach projektu jest studium odporności na błędy i awarie. W symulacjach będzie to rozwiązane przez założenie, że w którymś momencie jeden lub więcej z modułów przestanie reagować na komendy sterujące (np. na skutek wyczerpania się jego baterii lub jakiejś awarii), lub będzie reagował w sposób niezgodny z planem. Poprzez przeprowadzenie statystycznie znaczącej ilości symulacji, będzie możliwie wyciągnięcie wniosków dotyczących efektywności proponowanych rozwiązań i odporności systemu na błędy, która z oczywistych względów jest fundamentalna w systemach hiper-redundantnych. Poza symulacjami, można się spodziewać że praca z manipulatorem-demonstratorem wniesie pewną nową jakość do postrzegania tego zagadnienia. Jest wysoce prawdopodobne, że fizyczne urządzenie pokaże istnienie nowych problemów, które w idealnych symulacjach są trudne do przewidzenia. Doprowadzi to do odpowiedniej modyfikacji środowiska symulacyjnego jak i np. modyfikacji funkcji celu.
5. Literatura
[1] M. Zawidzki. Discrete Optimization in Architecture: Extremely Modular Systems. Springer, 2017.
[2] M. Zawidzki, K. Nishinari. Modular Pipe-Z system for 3D knots. J. Geom. Graph., 17(1):81–87, 2013.
[3] M. Zawidzki. Deployable Pipe-Z. Acta Astronautica, 127:20–30, 2016.
[4] M. Zawidzki and T. Nagakura. Arm-Z: a modular virtual manipulative. ICGG 2014, pp 75–80, Austria.
[5] Z. Zuo, Topology Optimization of Periodic Structures, PhD thesis, RMIT University, Australia, 2009.
[6] M. Beitelschmidt P. Koutsovasilis. Comparison of model reduction techniques for large mechanical systems. Multibody System Dynamics, 20(2):111-128, 2008.
[7] T. Sokół. A 99 line code for discretized michell truss optimization written in Mathematica. Structural and Multidisciplinary Optimization, 43(2):181-190, 2011.
[8] M. Zawidzki and J. Szklarski. Preliminary optimization of Pipe-Z reconfiguration. Proc. of the 5th Int. Conf. on Parallel, Distributed, Grid and Cloud Computing for Engineering, pp. 1–12, UK, 2017.
[9] M. Zawidzki and J. Szklarski. Transformations of Arm-Z modular manipulator with Particle Swarm Optimization. Advances in Engineering Software, 2017